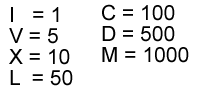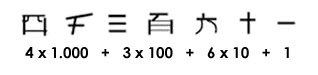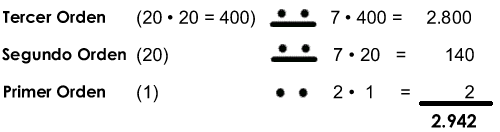TALLER SOBRE EL CONCEPTO DE CONJUNTOS

 

1- QUE SON CONJUNTOS

2- CUALES SON LOS ELEMENTOS DE LOS CONJUNTOS

3- CLASES DE CONJUNTOS

4- EJEMPLOS DE CADA CONJUNTO

 

OPERACIONES ENTRE CONJUNTOS

EJERCICIO

DETERMINAR LA CANTIDAD DE ESTUDIANTES DEL SIGUIENTE GRUPO:

 

FÚTBOL: F

NATACIÓN : N

FÚTBOL Y NATACIÓN: 7

SÓLO FÚTBOL: 13

SÓLO NATACIÓN: 4

NI NATACIÓN NI FÚTBOL: 6

 

ENCONTRAR LA CANTIDAD DE ESTUDIANTES DEL GRUPO, REALIZAR EL GRÁFICO DE VENN

 

RESOLVER EN EL CUADERNO

PROBLEMAS CON CONJUNTOS

 RESOLVER LOS SIGUIENTES EJERCICIOS 

1- Encontrar la intersección entre los siguientes conjuntos:

 

M= { X/X es un número primo menor que 20} y N= {x/x es un número par menor que 10}

 

2- En un restaurante 12 personas almuerzan plato principal, 7 personas almuerzan entrada y 5 personas almuerzan plato principal y entrada.  ¿Cuántas personas almorzaron solo una opción en el restaurante  

SISTEMAS DE NUMERACIÓN

Es habitual que, cuando pensamos en las operaciones aritméticas, nos remitimos sólo al sistema decimal que se usa en la vida diaria. Sin embargo, existen otros muchos sistemas de numeración, algunos de los cuales forman parte también de las actividades cotidianas. Así, el sistema binario es básico en el funcionamiento de los ordenadores, y el sexagesimal se utiliza para medir los valores de los ángulos y el cómputo del tiempo de los relojes, entre otras tareas.

Elementos de los sistemas de numeración

En esencia, un sistema de numeración puede definirse como un conjunto de signos, relaciones, convenios y normas destinados a expresar de modo gráfico y verbal el valor de los números y las cantidades numéricas.

En la actualidad, se usan predominantemente sistemas de numeración de carácter posicional, donde cada numeral o guarismo representa un valor distinto según la posición que ocupa en la cadena numérica (por ejemplo, el numeral 1 significa unidad en la cantidad 1, pero es decena en 13, centena en 148, etcétera).

En un sistema de numeración se contemplan varios elementos fundamentales:

 

  • La base del sistema, que se define como un convenio de agrupación de sus unidades. Por ejemplo, la base 10 o decimal agrupa diez unidades, mientras que la binaria únicamente agrupa dos.
  • Los numerales del sistema, o cifras elementales que se utilizan, según la base. En el sistema decimal, se usan los numerales 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. En cambio, en el sistema binario tan sólo se emplean el 0 y el 1.
  • Las normas de combinación de los numerales para formar los números. Según ello, a cada cifra se le asocian dos propiedades: su valor absoluto intrínseco y su valor posicional o relativo, que depende de la posición que ocupa en la cantidad numérica

DEBEN ESCRIBIR EN EL CUADERNO CON CIFRAS:

1- CUATROCIENTOS QUINCE MIL DOSCIENTOS DOS

2- SETECIENTOS CINCUENTA Y OCHO MIL CUATROCIENTOS

3- DOS MILLONES NOVECIENTOS MIL

ORDENAR DE MAYOR A MENOR LOS SIGUIENTES NÚMEROS

617.751.860

617.800.003

70.998.567

618.003. 703

REALIZAR LAS SIGUIENTES OPERACIONES:

348.798 + 678.904

398.997 - 69.632

54.535 X 908

65.400 / 2

DIFERENTES SISTEMAS DE NUMERACIÓN 

A lo largo de la historia de la humanidad, el ser humano ha buscado diferentes maneras de representar cantidades. Si nos remontamos hacia más de dos mil años, los pueblos de aquella época no utilizaban números para contar objetos, sino que hacían uso de cualquier elemento que pudiera servirles para contar, ya sea utilizando sus propios dedos, dibujando símbolos, marcando bastones (ramas) o haciendo nudos en una cuerda, entre otros.

el primer uso que se le dio a los números, se relaciona con la necesidad de ordenar elementos, no con la de contar o medir objetos.

A continuación veremos los 5 sistemas de numeración más característicos de la historia, reconociendo sus elementos principales y los símbolos que ellos utilizaron para representar las cantidades indicadas.

SISTEMA DE NUMERACIÓN EGIPCIO (3000 A.C.)

Si hay algo que hasta el día de hoy sigue vigente es la cultura egipcia. Esto no se debe meramente al azar, sino que responde al gran legado cultural que nos dejaron, ya sea por sus monumentales construcciones como por sus conocimientos y descubrimientos en agricultura, arte y matemáticas.

En relación con éste último, podemos ver que se los egipcios se vieron enfrentados a la necesidad de realizar cálculos y considerar dimensiones para, por ejemplo, llevar a cabo sus construcciones, situación que los desafió a encontrar algún modo de representar las cantidades utilizadas. Además, vemos que representaron las cifras utilizadas en papiros, dándoles a éstas un uso práctico, relacionados principalmente con la geometría y la aritmética.

Los egipcios tenían un sistema de numeración decimal (contaban de 10 en 10, lo cual se asocia con que tengamos 10 dedos), no utilizaban símbolos para representar el cero y realizaban jeroglíficos que les permitían identificar el orden en que se agrupaban las unidades en las cuales estaban trabajando.

Por otro lado, ellos utilizaban un procedimiento aditivo para representar los números, en donde acumulaban todos los signos pertenecientes al número que querían representar y formaban con ello el número.

Es importante mencionar que el orden en que se escribían los símbolos utilizados les era indiferente, debido a que cada figura representaba exclusivamente un único valor. De esta manera, independiente del orden en que éstos se presentaban, el valor no cambiaba. Es decir, su representación podía realizarse de izquierda a derecha, de abajo hacia arriba y viceversa, sin alterar el valor de la cifra mencionada.

SISTEMA

DE NUMERACIÓN GRIEGO (600 A.C.)

Utilizaron letras del alfabeto griego para representar las cantidades.

El sistema de numeración griego más antiguo fue el ático o acrofónico, que era derivado del sistema de numeración romano, cuyos símbolos eran:

Figura: Sistema de Numeración Griego: Ático o acrofónico

Vale mencionar que los números 50, 500 y 5.000, se obtenían agregando el signo de 10, 100 ó 1.000 al de 5.

Así por ejemplo, para obtener el número 50 el símbolo utilizado era el del 5 y el de 10, dando como resultado el símbolo que representaba 50, y que puedes apreciar en la figura anterior.

Considerando el caso descrito, podemos ver que junto con un principio aditivo, en el sistema de numeración griego se combina el principio multiplicativo.

Sin embargo, a partir del siglo IV a.C. este sistema fue sustituido por el jónico, el cual utilizaba las 24 letras del alfabeto griego, junto con algunos otros símbolos, tal como muestra la siguiente figura.

Figura: Sistema de Numeración Griego: Jónico

En este sistema a cada cifra de la unidad se le asignaba una letra, a cada decena otra letra y a cada centena otra. Es decir, se basó en un principio de adición, en donde los valores numéricos que adoptaban las letras se sumaban para formar el total. Por ejemplo el 242 se representaba como ??b (200 + 40 + 2).

Con esto, los números parecen palabras, ya que están compuestos por letras, y éstas a su vez, tienen un valor numérico.

SISTEMA DE NUMERACIÓN ROMANO

Si existe un sistema de numeración que ha perdurado en el tiempo, ese es el romano. Actualmente lo utilizamos para numerar capítulos o escenas de una obra de teatro, para designar el nombre de algunas autoridades (como emperadores, reyes y papas), para ordenar los contenidos de un índice y los tomos de una enciclopedia, entre otros.

En relación con los símbolos que los romanos utilizaron para representar cantidades, fueron letras mayúsculas, que en nuestro sistema de numeración equivalen a un número específico. Así tenemos,

Figura: Sistema de Numeración Romano

Ahora bien, para representar cantidades con números romanos, es importante que tener en consideración ciertas reglas guían su escritura.

SISTEMA DE NUMERACIÓN CHINO (1500 A.C.)

La cultura china es indudablemente una de las más completas y antiguas de la humanidad. Su legado perdura hasta la actualidad, ya que han sido gestores de grandes descubrimientos, realizando aportes importantes para la humanidad.

En relación con el sistema de numeración que ellos utilizaron, éste era decimal, en donde utilizaron las unidades y las distintas potencias de 10 para representar cantidades. Tenían 9 símbolos distintos para los primeros 9 números pero ningún símbolo para representar el cero.

Los símbolos eran:

Sistema de Numeración Chino

Su representación de los números se basó en un principio multiplicativo y era de carácter posicional, por lo que dependiendo de la posición que tenía el símbolo (cifra) en el número, el valor que éste iba a tener.

Como podemos ver, el sistema de numeración chino tiene semejanzas con el que utilizamos nosotros actualmente, sin embargo, tanto los símbolos con que representan cantidades, como la orientación que los números pueden adquirir en una cifra, es distinta. Además, vemos que su disposición es híbrida, es decir, a la hora de componer los números emplean tanto la multiplicación como la adición, por lo que cada cifra es acompañada por otra que la multiplica, y en donde la suma total de dichas multiplicaciones da la cifra total.

Veamos en un ejemplo:

El número 4.361 se representa así:

Ejemplo: Ejemplo de Números Chinos

Actualmente, utilizan el mismo sistema de numeración, cuyos símbolos son los que vimos anteriormente, y donde prima el carácter multiplicativo y posicional de los símbolos que se disponen.

SISTEMA DE NUMERACIÓN MAYA

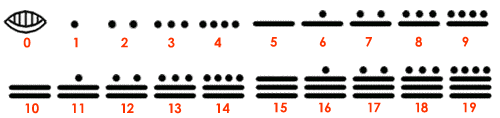
Uno de los aspectos que más destacan en el sistema de numeración Maya es que ellos simbolizaron el cero. Vemos también que éste era de carácter posicional y en base 20, utilizando principalmente rayas y puntos para simbolizar los números. En donde el caracol representaba al cero, los puntos al 1 y la raya al 5.

En cuanto a la disposición de las cifras, vemos que éstas se escriben verticalmente y con las unidades en la parte inferior. Además agruparon símbolos hasta el 19, asignando a los números mayores un valor según la posición en que se encuentran. Los símbolos con que representaron los números hasta el 19 son:

Figura: Sistema de Numeración Maya

Analizando los símbolos que se presentan, podemos ver que el número 14 está formado por 2 rayas y 4 puntos. Como las rayas representan al 5 y los puntos al 1, multiplicaremos 2×5 y 4×1, obteniendo un total de 10 + 4, es decir, 14.

Ahora bien, para escribir números iguales o superiores al 20, las cifras adquirían un valor que dependía de la posición en donde se encontraban, disponiéndose en columnas y asignándose un valor de abajo hacia arriba, en el que hay que multiplicar el valor de cada cifra por 1, 20, 20×20, 20x20x20… según el lugar que ocupe. Por ejemplo:

Figura: Ejemplo Sistema de Numeración Maya

SISTEMA DE NUMERACIÓN INCA

Poseían un sistema de numeración decimal y de carácter posicional. Como no hicieron uso de la escritura no dejaron un registro gráfico de símbolos que permitan interpretar cantidades, sin embargo, los Incas se vieron en la necesidad de registrar los cálculos que iban realizando, por lo que utilizaron el quipu.

El quipu era un instrumento que poseía cuerdas y que, mediante la realización de nudos de variados colores y tamaños, les permitió registrar la información numérica que iban obteniendo.

ENTRAR AL SIGUIENTE LINK Y LEER SOBRE SISTEMA BINARIO

http://platea.pntic.mec.es/~lgonzale/tic/binarios/numeracion.html#Sistema_de_numeraci%F3n_binario.

CONSULTAR Y ESCRIBIR EN EL CUADERNO SOBRE OPERACIONES CON NUMEROS BINARIOS

EJERCICIOS CON NUMEROS ROMANOS

 

PASAR LOS SIGUIENTES NUMEROS A NUMEROS ROMANOS

 

57

370

500

1356

2768

278

5000

4000

 

CDLIX

DL

M

D

C

IIX